Hauptinhalt
Topinformationen

Kontakt
Prof. Dr. Holger Brenner
Tel.: +49 541 969 2507
Fax.: +49 541 969 2770
hbrenner@uni-osnabrueck.de
am 19.06.2015
ab 9:30 Uhr besuchten etwa 450 Schülerinnen und Schüler ab Jahrgangstufe 10 das mathematische Institut der Universität. Sie hörten Vorträge, arbeiteten selbst in verschiedenen Workshops und informierten sich bei der Fachschaft und der zentralen Studienberatung.
Zwei Schüler stellten ihre Facharbeiten vor, die sie im Seminarfach Mathematik geschrieben haben. Die Arbeiten wurden mit einem Buchpreis ausgezeichnet.
Eindrücke vom Tag der Mathematik, Neuen Osnabrücker Zeitung
Fotos vom Tag der Mathematik
Topinformationen
Vorträge
9:30 Uhr Begrüßung durch das Präsidium und den Fachbereich.
Einführung in den Tag.

Warum Mathematik studieren?
Prof. Dr. O. Röndigs (nach der Begrüßung)
Viele Berufe, wie etwa LehrerIn, ÄrztIn oder TaxifahrerIn, kann man sich gut vorstellen. Aber was ist der Beruf des Mathematikers? Auf der Suche nach einigen Antworten soll insbesondere geklärt werden, auf welche Arten man an der Universität Osnabrück Mathematik studieren kann, und welche Berufsmöglichkeiten ein Studium der Mathematik nach sich zieht.
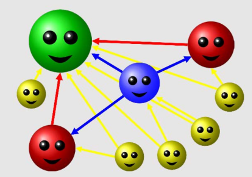
Das 1x1 von Google
Torsten Görner (10:30 Uhr)
In der heutigen Zeit entsteht häufig der Eindruck, dass eine Google-Suche zielführender als das selbstständige Nachdenken ist. Um zu verstehen, wie die Ergebnisse zustande kommen, müssen wir ein wenig Mathematik betreiben. Wir lernen dabei etwas über Graphen und wie sich deren Eigenschaften mit Hilfe von Matrizen bestimmen lassen.
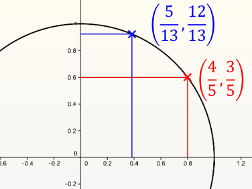
Pythagoreische Tripel und der Einheitskreis
Prof. Dr. H. Brenner (11:30 Uhr)
Ein pythagoreisches Tripel ist ein Tupel (a,b,c) aus ganzen Zahlen, die die Bedingung a2+b2=c2 erfüllen,also als Seitenlängen eines rechtwinkligen Dreiecks auftreten. Das bekannteste Beispiel ist (3,4,5), ein weiteres ist (5,12,13). Ist es möglich, sich eine Übersicht über alle pythagoreischen Tripel zu verschaffen? Im Vortrag werden wir diese Frage beantworten, wobei wir zahlentheoretische, algebraische und geometrische Argumentationsweisen verwenden, die für das Mathematikstudium typisch sind.
Workshops
Jeweils um 10:30 Uhr und 11:30 Uhr werden folgende Workshops angeboten:

Knifflige Knoten
Man nehme einen Schnürsenkel und binde ihn zu einem Knoten. Dann klebe man die Enden der Schnur zusammen und erhalte so einen mathematischen Knoten. Eigentlich ist es ja ein Kreis, aber irgendwie verknotet. Die zentrale Frage der Knotentheorie ist es zu bestimmen, wann zwei Knoten gleich sind. Einfach formuliert, aber in der Praxis schwer zu beantworten. Wir werden uns verknoten und die Reidemeisterbewegungen nutzen, um uns zu entknoten.

Mathematica
Es geht um Algebra und Geometrie. Wie kann man Gleichungen visualisieren? Kann man geometrische Gebilde durch Gleichungen beschreiben? Ebenen werden durch lineare Gleichungen wie 2x+y+3z-5=0 beschrieben. Interessanter sind die Flächen, die durch nicht lineare Gleichungen definiert sind. Wir wollen mit dem CAS Mathematica experimentieren und die Bilder von Flächen erzeugen.
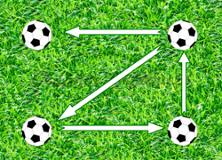
Isomorphe Fußballgruppen
Jedes Fußballspiel, jede Fußballweltmeisterschaft, jede Vorrundengruppe ist einzigartig. Oder doch nicht? Welche und wie viele Konstellationen gibt es bei einer Vorrundengruppe mit vier Mannschaften, wenn man sich nur für die Gewinnstruktur interessiert?

Die Welt erobern mit Risiko
Bei dem Brettspiel Risiko lautet das Motto: Erobere die Welt! Wer dabei die beste Strategie besitzt, hat die besten Chancen, sein Ziel zu verwirklichen.
In diesem Workshop werden wir die einzelnen Spielzüge analysieren und mit Hilfsmitteln der Wahrscheinlichkeitstheorie optimale Strategien bestimmen.

Bierdeckel stapeln - ganz schön schräg
Einen beliebigen hohen Turm aus Bierdeckeln zu stapeln ist einfach - vorausgesetzt, dass kein Wind weht und genug Deckel zur Verfügung
stehen. Wie sieht es aber aus, wenn man einen schrägen Stapel auftürmt, um einen möglichst großen Überhang zu erzeugen? Stößt man da irgendwann an eine natürliche Grenze, oder kann man mit der richtigen Stapelstrategie einen beliebigen Überhang erzeugen?

Wie man Musik anschaut
Musik wie auch alle anderen Geräusche bestehen aus sich zeitlich verändernden Schallwellen. Wir fassen diese als Funktion der Zeit auf und zerlegen
sie in mathematische Grundbausteine. Wir lernen, dass Musiknoten durchaus eine geeignete Kodierung für Musik darstellen und wieso der Kammerton a1 auf verschiedenen Instrumenten unterschiedlich klingt. Musikinstrumente sind herzlich willkommen.

Penrose-Pflasterungen
Penrose-Pflasterungen sind nicht-periodischePflasterungen der Ebene. Nicht-periodisch bedeutet,dass eine verschobene Kopie nie deckungsgleich mitdem Original ist. Außerdem tritt in einer Penrose-Pflasterung jedes Teilmuster unendlich oft auf. Wirwerden solche Pflasterungen ausprobieren.
Präsentation von Facharbeiten
Die ausgezeichneten Facharbeiten werden von ihren AutorInnen vorgestellt. So können Sie von SchülerInnen und Schülern mathematische Sachverhalte erfahren und im Anschluss Fragen stellen. Eine anschließende Diskussion über Themen von mathematischen Facharbeiten ist erwünscht.
LehrerInnenworkshop
Kooperationsmöglichkeiten zwischen Schule und Universität
In einer offenen Diskussion sollen Möglichkeiten der
Zusammenarbeit zwischen Schule und Universität beispielsweise im Bereich Facharbeiten oder Fortbildungen erörtert werden. Alle TeilnehmerInnen sind eingeladen, eigene Erfahrungen, Wünsche und Vorstellungen in
das Gespräch mit einzubringen.

